Как рассчитать стандартное отклонение в excel

Как выделить максимальное значение в Excel

В ситуации, когда вы хотите определить самое большое число в исходном наборе данных, самый быстрый способ – выделить его с помощью условного форматирования Excel. Приведенные ниже примеры покажут вам два разных варианта действий.

Выделите максимальное число в диапазоне

В Microsoft Excel есть предопределенное правило для форматирования максимальных чисел в диапазоне, которое идеально соответствует нашим потребностям. Вот как можно применить его:

1. Выберите диапазон чисел (в нашем случае C2: E8).
2. На вкладке «Главная» в группе «Стили» щелкните «Условное форматирование»> «Новое правило».
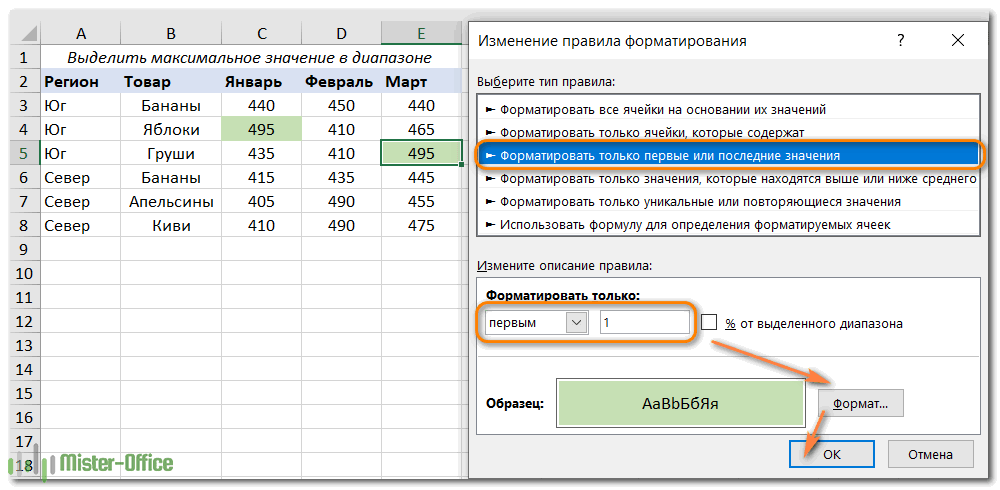
3. В диалоговом окне «Новое правило форматирования» выберите «Форматировать только первые или последние значения».
4. На нижней панели выберите «первым» из раскрывающегося списка и введите 1 в поле рядом с ним (это означает, что вы хотите выделить только одну ячейку, содержащую наибольшее значение).
5. Нажмите кнопку «Формат» и выберите стиль оформления.
6. Дважды щелкните OK, чтобы закрыть оба окна.

Как выделить цветом максимальное значение в каждой строке

Поскольку нет встроенного правила, чтобы выделить наибольшее значение из каждой строки, вам придется настроить собственное на основе функции МАКС. Вот как:

1. Выберите все строки, которые вы хотите проверить (C3:E8).
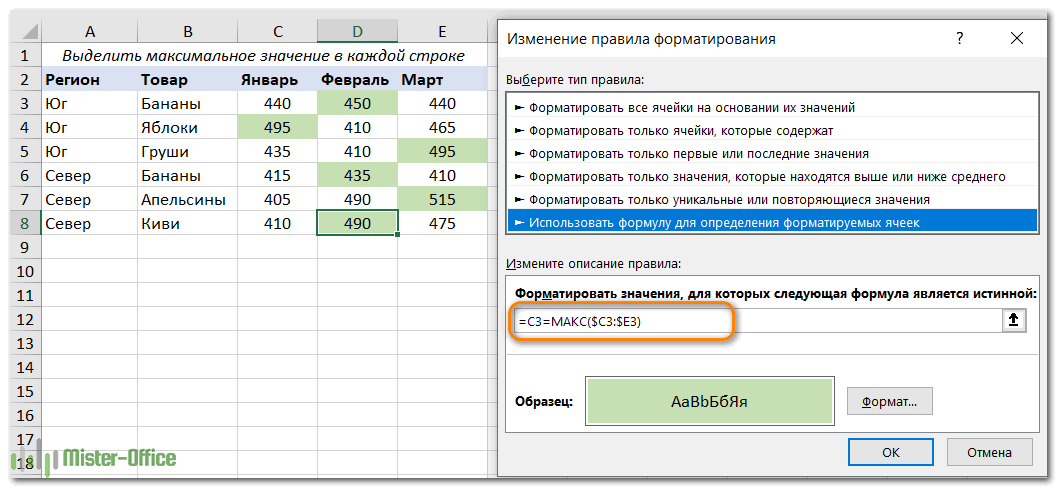
2. Кликните Новое правило > Использовать формулу.
3. В поле Форматировать значения, запишите:

Где C3 — крайняя верхняя левая ячейка, а $C3:$E3 — координаты первой строки. Чтобы правило работало, обязательно зафиксируйте координаты столбца в диапазоне знаком $.

1. Нажмите кнопку «Формат» и выберите нужный формат.
2. Дважды щелкните ОК.

Кончик. Таким же образом вы можете выделить максимальноезначение в каждом столбце. Шаги в точности такие же, за исключением того, что вы пишете условие для диапазона первого столбца и фиксируете координаты строки:

Дополнительные сведения см. В разделе « Как создать правило условного форматирования на основе формул» .

Что такое стандартное отклонение в статистике и что оно позволяет нам знать?

Стандартное или стандартное отклонение как также известно, является статистическая мера что позволяет вам узнать информацию о средняя дисперсия переменной, так что очень интересно когда хочешь узнать насколько значения отклоняются от среднего значения

Важно отметить, что стандартное отклонение всегда больше или равно нулю,. Чтобы ясно понять эту концепцию, необходимо проанализировать две концепции об отклонениях, такие как следующие:. Чтобы ясно понять эту концепцию, необходимо проанализировать две концепции об отклонениях, такие как следующие:

Чтобы ясно понять эту концепцию, необходимо проанализировать две концепции об отклонениях, такие как следующие:

• Отклонение: Это разделение, которое существует между оценить любой из ряда и среднее или среднее как это еще называется.
• Математическое ожидание, среднее или ожидаемое значение: Это среднее из серия образцов данных,

Зная эти два термина, можно сказать, что стандартное отклонение будет рассчитываться аналогично среднему, но на этот раз они взяты значения отклонения, Хотя это рассуждение логично и интуитивно понятно, есть сбой, который можно проверить с помощью следующего изображения.

Как видно, на указанном изображении представлено 6 значений наблюдаются, это означает, что N = 6, среднее значение наблюдений представлено черной линией, расположенной во всем центре графика, оно имеет значение 3. Следовательно, знание среднего можно понять отклонение разница между любым из наблюдений и черной линией.

Это означает, что существует 6 наблюдений, поэтому для каждого из них необходимо выполнить следующую процедуру:

• Отклонение а (2-3) = -1
• Отклонение а (4-3) = 1
• Отклонение а (2-3) = 1
• Отклонение а (4-3) = 1
• Отклонение а (2-3) = -1
• Отклонение а (4-3) = 1

Если вы можете увидеть, когда Вы добавляете два отклонения, 6 отклонений и делим на N = 6, результат заканчивается нуль. Логика будет в том, что среднее отклонение из 1, но математическая характеристика среднего по отношению к ценности, которые формируют это, чем сумма отклонений равна нулюДля того, чтобы решить это, необходимо возвести в квадрат отклонения.

Что измеряет стандартное отклонение?

Представьте, что вы владелец двух магазинов

И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель

Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.

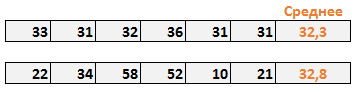
Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.

Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке. Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.

В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.

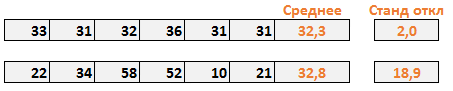
В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2). Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных. То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.

В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе. Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять. Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.

Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.

Что такое стандартное отклонение в Excel?

Например: предположим, что у вас есть точки данных 5, 3, 6, 8 и 10.

1. Всего точек данных: 5
2. Сумма точек данных: 32
3. Среднее (среднее) = 32/5 = 6,4
4. Стандартное отклонение Excel = 2,7

Это означает, что диапазон большинства точек данных находится в пределах 2,7 от среднего значения, т. Е. От 3,7 до 9,1 (по обе стороны от среднего значения 6,4).

• Если значение стандартного отклонения ниже, то частота точек данных ближе к среднему (среднему) значению.
• Если значение стандартного отклонения выше, то частота точек данных больше среднего (среднего) значения.

Рассчитать стандартное отклонение в Excel

Когда мы имеем дело с количественными данными, мы всегда ищем типичный элемент набора данных. Что находится в середине точки данных? т.е. среднее значение или среднее значение точек данных.

Среднеквадратичное отклонение помогает нам понять, насколько разрознены данные. Данные о ценах используются в качестве меры волатильности, особенно в финансовой сфере.

Ниже приведены примеры, которые позволят нам понять концепцию стандартного отклонения Excel на практике.

Ниже приведены оценки уровня квалификации сотрудников компании. Из этого набора данных нам нужно рассчитать значение стандартного отклонения.

Выполните следующие шаги, чтобы рассчитать Стандартное отклонение в Excel.

Шаг 1: Рассчитайте среднее значение (среднее) данных в Excel.

Среднее = 55,2

Таким образом, среднее значение данных составляет 55,2, т.е. средний балл уровня квалификации сотрудников составляет 55,2.

Шаг 2: Вычислите разницу оценок каждого сотрудника от среднего значения и найдите разницу.

Дисперсия =

Дисперсия =

Дисперсия = 3,36

Шаг 3: Рассчитать SD (стандартное отклонение в Excel)

SD — это просто квадратный корень из Дисперсия.

SD = 1,83

Заключение: Итак, история этого расчета заключается в том, что диапазон оценок сотрудников варьируется от 53,37 до 57,03.

Формулы стандартного отклонения в Excel

В Excel у нас есть всего 8 типов формул стандартного отклонения в Excel.

Эти 8 формул находятся в двух группах Выборка и популяция.

STDEV.S, STDEVA, STDEV, DSTDEV находится под Образец.

СТАНДОТКЛОН.P, СТАНДОТКЛОНП, СТАНДОТКЛОНПА, DSTDEVP находится под Численность населения.

• численность населения означает, что вы рассматриваете весь набор данных.
• Образец означает, что очень сложно использовать все данные, и вы берете только образец набора данных.

Мы можем использовать выборочные данные для всего набора данных, чтобы вычислить стандартное отклонение и сделать выводы для всего набора данных.

• Практически во всех случаях мы используем формула СТАНДОТКЛОН. S для расчета стандартного отклонения в excel. Это используется, когда мы хотим использовать только числовые значения и игнорировать текстовые значения.
• Если вы вообще хотите использовать текстовые значения в диапазоне, используйте СТАНДОТКЛОН. Он принимает значения text и FALSE как 0 и TRUE как 1.

Использование формулы STDEV.S для стандартного отклонения в Excel

Формула STDEV.S в excel включает только числа.

• Номер 1: Первое значение выборки всей генеральной совокупности. Здесь вы можете выбрать диапазон.
• Номер 2: Необязательный аргумент. Если вы охватили весь диапазон данных выборки, это становится необязательным.

Как использовать функцию STDEV.S в Excel?

Ниже приведены данные о росте козла, а ниже — рост каждой козы на уровне плеч.

Вы можете скачать этот шаблон Excel со стандартным отклонением здесь — Шаблон Excel со стандартным отклонением

Примечание: высота указана в миллиметрах.

Шаг 1: Рассчитайте среднее значение, т. Е. Среднее значение.

Шаг 2: Примените СТАНДОТКЛОН.S в формуле Excel к диапазону B2: B6.

Таким образом, стандартное отклонение роста козла составляет 165 (ближайшее к миллиметру).

Значение 165 миллиметров означает, что большая часть роста козы будет в диапазоне от 229 до 559 миллиметров.

Это обе стороны от среднего значения, то есть 394 — 165 = 229 и 394 + 165 = 559.

Примечание. Это стандартное отклонение для большинства коз, что означает, что только некоторые из них находятся в этом диапазоне роста. Когда мы применим формулу к большим наборам данных, мы увидим большую разницу.

То, что нужно запомнить

• В STDEV.S в excel буква «S» представляет собой образец набора данных.
• Он будет игнорировать текстовые значения.
• STDEVA учитывает как текстовые, так и числовые значения. ИСТИНА = 1 и ФАСЛ = 0.
• Выборка означает лишь несколько элементов большой совокупности.
• Должно быть как минимум два числовых значения.
• S доступен с 2010 года и более поздних версий. В более ранних версиях STDEV — это формула.

УЗНАТЬ БОЛЬШЕ >>

Excel STDEVA Function

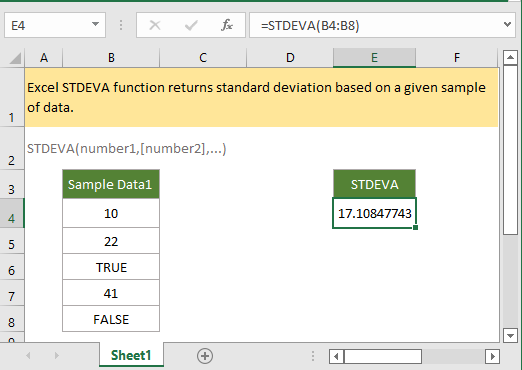
Если вы хотите следовать этому руководству, загрузите пример электронной таблицы.

Описание

Excel STDEVA Функция возвращает стандартное отклонение на основе выборки населения. Его можно использовать для измерения того, насколько широко значения разбросаны по сравнению со средним значением. В отличие от функции СТАНДОТКЛОН.С, функция СТАНДОТКЛОН оценивает логические значения и текст, которые появляются в ссылке.

Синтаксис формулы

СТДЕВА(number1, , …)

аргументы

Возвращаемое значение

Наблюдения и советы этой статьи мы подготовили на основании опыта команды STDEVA функция возвращает числовое значение.

замечание

1. Аргументы функции СТАНДОТКЛОН представляют собой выборку совокупности, если данные представляют всю совокупность, функция СТАНДОТКЛОНПА может быть более подходящей.

2. Функция STDEVA с использованием метода «n — 1» для расчета.

3. Аргументы могут быть числами или именами, массивами или ссылками, содержащими числа, текстовыми представлениями чисел или логическими значениями (ИСТИНА и ЛОЖЬ) в ссылке.

4. Функция STDEVA принимает логическое значение TURE как 1, FALSE как ноль.

5. Пустые ячейки и текстовые значения игнорируются, если ИСТИНА и ЛОЖЬ введены непосредственно в массив, они игнорируются функцией СТАНДОТКЛОН.

6. Аргументы, которые являются ошибочными значениями или текстами, не могут быть преобразованы в числа, вызовут ошибки.

7. Функция STDEVA использует следующее уравнение:

где

X — среднее значение выборки, n — размер выборки.

Использование и примеры

Пример: основное использование

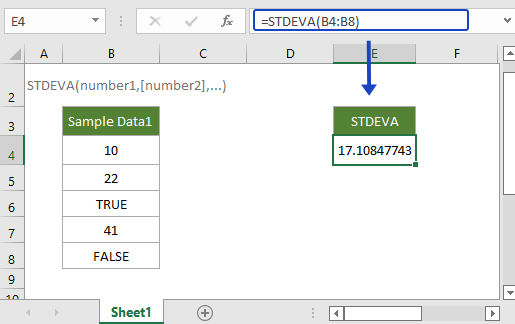
Имеется столбец B4:B8, содержащий совокупность данных. Чтобы получить стандартное отклонение, используйте следующую формулу:

=STDEVA(B4:B8)

Нажмите Enter ключ, чтобы получить стандартное отклонение.

Функции стандартного отклонения в Excel

Функция	Набор данных	Текст и логика
STDEV	Образец	Игнорируется
STDEV.S	Образец	Игнорируется
STDEVP	Население	Игнорируется
STDEV.P	Население	Игнорируется
STDEVA	Образец	Оценивается
STDEVPA	Население	Оценивается

Относительные функции:

Excel STDEV ФункцияФункция Excel СТАНДОТКЛОН возвращает стандартное отклонение на основе заданной выборки данных.

Excel STDEV.P ФункцияФункция Excel STDEV.P возвращает стандартное отклонение на основе всей совокупности. Его можно использовать для измерения того, насколько широко значения разбросаны по сравнению со средним значением.

Excel STDEV.S ФункцияФункция Excel СТАНДОТКЛОН.С возвращает стандартное отклонение на основе заданной выборки данных.

Excel PERMUT ФункцияФункция Excel ПЕРЕСТАНОВКА возвращает количество перестановок заданного количества объектов из набора объектов.

Дополнительная информация

Функция STDEVPA возвращает стандартное отклонение генеральной совокупности, значения которой содержатся на листе Excel и заданы аргументами в STDEVPA.

Синтаксис

Параметры (value1, value2, value 3,…) имеют до 30 аргументов значений.

Часто STDEVPA включает только один аргумент значения, указывающий диапазон ячеек, содержащих образец. Например:

Пример использования

STDEVPA отличается от STDEVP только тем, как он обрабатывает ячейки в диапазоне данных, содержащие ИСТИНА, ЛОЖЬ или текстовую строку. STDEVPA интерпретирует TRUE как значение 1 и false как значение 0. Он интерпретирует текстовую строку как значение 0. Пустые ячейки игнорируются. Эти интерпретации также применяются к функциям COUNTA, AVERAGEA и STDEVA.

ФУНКЦИЯ STDEVP игнорирует пустые ячейки и ячейки, содержащие true, FALSE или текстовую строку. Эти интерпретации также применяются к функциям COUNT, AVERAGE и STDEV.

Используйте STDEVP вместо STDEVPA, если вы не уверены, что функция интерпретирует строки TRUE, FALSE и текстовые строки, как описано выше в этой статье для STDEVPA. Большинство данных, для которых требуется вычислить стандартное отклонение генеральной совокупности, полностью числовые. Поэтому stDEVP подходит.

Чтобы продемонстрировать разницу между STDEVPA и STDEVP, создайте пустой лист Excel, скопируйте приведенную ниже таблицу, выберите ячейку A1 на пустом листе Excel, а затем щелкните «Вставить» в меню «Правка», чтобы записи в таблице ниже заполняли ячейки A1:D12 на листе.

A	Б	В	D
Данные
6	6	Пример среднего значения для STDEVP, STDEV	=СРЗНАЧ(A1:A8)
4	4	Размер образца для STDEVP, STDEV	=COUNT(A1:A8)
2	2	СТАНДОТКЛОНП	=STDEVP(A1:A8)
1	1	STDEV	=STDEV(A1:A8)
7	7	Пример среднего значения для STDEVPA, STDEVA	=СРЗНАЧА(A1:A8)
TRUE	1	Размер образца для STDEVPA, STDEVA	=COUNTA(A1:A8)
		STDEVPA	=STDEVPA(A1:A8)
		СТАНДОТКЛОНА	=STDEVA(A1:A8)
		STDEVP для столбца B	=STDEVP(B1:B8)
		STDEV для столбца B	=STDEV(B1:B8)

Примечание.

После вставки этой таблицы на новый лист Excel нажмите кнопку «Параметры вставки» и выберите «Сопоставление форматирования назначения». Выбрав вставленный диапазон, наведите указатель мыши на пункт «Столбец» в меню «Формат» и выберите пункт «Автоподбор выделения».

В этом примере ячейки A1:A8 содержат значения данных, которые контрастют между STDEVPA и STDEVP. Все функции, используемые в ячейках D3:D10, ссылаются на данные в A1:A8. STDEVPA обрабатывает текстовую строку в ячейке A1 как значение 0, числовые значения в A3:A7 как себя, а значение TRUE в A8 как 1. Значения, используемые для STDEVPA в A1:A8, отображаются в B1:B8. На листе показано, что значение STDEVPA(A1:A8) в ячейке D9 точно равно значению STDEVP(B1:B8) в ячейке D11.

STDEVP и STDEVPA возвращают стандартное отклонение генеральной совокупности, тогда как STDEV и STDEVA возвращают стандартное отклонение выборки. Во всех версиях Excel значение сначала вычисляется для VAR, VARA, VARP или VARPA. Квадратный корень этого значения возвращается (соответственно) для STDEV, STDEVA, STDEVP или STDEVPA. Для оценки VAR, VARA, VARP и VARPA Excel 2003 вычисляет количество точек данных и их среднее значение, а затем вычисляет сумму квадратных отклонений значений данных из этого среднего значения. Эта сумма квадратных отклонений является числовым значением дробной части, используемой для оценки VAR, VARA, VARP и VARPA. Знаменателем для VARP и VARPA является количество точек данных. Знаменатель для VAR и VARA на единицу меньше числа точек данных.

Чтобы вычислить каждую из этих четырех функций, Excel 2003 и Excel 2007 используют процедуру, которая отличается от процедуры, используемой в предыдущих версиях Excel, и улучшает ее. Статья для STDEV содержит лист, который позволяет изучить случаи, когда в STDEV возникает необычное поведение для более ранних версий Excel, но не для Excel 2003 или Excel 2007. Однако такие случаи могут возникать только в крайних ситуациях. Процедуры для STDEV, STDEVA, STDEVP, STDEVPA, VAR, VARA, VARP и VARPA были изменены таким же образом, чтобы улучшить числовую стабильность результатов. Эти изменения также описаны в статьях о STDEV и VAR.

Дополнительные сведения см. в следующих статьях:

Example

Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.

Стандартное отклонение – это статистический инструмент, который приблизительно показывает, насколько в среднем каждое число в списке значений данных отличается от среднего значения или среднего арифметического самого списка.

Инструкции в этой статье относятся к Excel 2019, 2016, 2013, 2010, 2007; Excel для Mac, Excel для Office 365, Excel Online, Excel для iPad, Excel для iPhone и Excel для Android.

Практическое использование функции STDEV

В Excel функция STDEV обеспечивает оценку набора стандартных отклонений данных. Функция предполагает, что введенные числа представляют только небольшую часть или выборку из всей изучаемой популяции. В результате функция STDEV не возвращает точное стандартное отклонение. Например, для чисел 1 и 2 функция STDEV в Excel возвращает приблизительное значение 0,71, а не точное стандартное отклонение 0,5.

Несмотря на то, что функция STDEV оценивает только стандартное отклонение, функция полезна, когда тестируется только небольшая часть совокупности. Например, при тестировании готовой продукции на соответствие среднему значению (для таких мер, как размер или долговечность) тестируется не каждая единица, и это дает оценку того, насколько каждая единица во всей совокупности отличается от средней.

Чтобы показать, насколько близки результаты для STDEV к фактическому стандартному отклонению (с использованием приведенного выше примера), размер выборки, использованный для функции, был менее одной трети от общего объема данных. Разница между расчетным и фактическим стандартным отклонением составляет 0,02.

STDEV в синтаксис и аргументы Excel

Синтаксис функции относится к макету функции и включает имя функции, скобки, разделители запятых и аргументы. Синтаксис для функции стандартного отклонения:

Number1 (обязательно). Это число может быть фактическим числом, именованным диапазоном или ссылкой на ячейку для расположения данных на листе. Если используются ссылки на ячейки, пустые ячейки, логические значения, текстовые данные или значения ошибок в диапазоне ссылок на ячейки игнорируются.

Number2, … Number255 (необязательно): можно ввести до 255 номеров.

Пример функции STDEV

В этом руководстве образец данных, используемый для аргумента Number функции, находится в ячейках с A5 по D7. Стандартное отклонение для этих данных будет рассчитано. Для сравнения включены стандартное отклонение и среднее значение для всего диапазона данных от A1 до D10.

В Excel 2010 и Excel 2007 формула должна быть введена вручную.

Выполните следующие шаги, чтобы выполнить задачу и рассчитать информацию с помощью встроенной функции:

Выберите ячейку D12 , чтобы сделать ее активной. Здесь будут отображаться результаты функции STDEV.

Введите функцию = STDEV (A5: D7) и нажмите Enter .

Значение в D12 изменяется до 2,37. Это новое значение представляет собой расчетное стандартное отклонение каждого числа в списке от среднего значения 4,5

Для более старых версий Excel введите формулу вручную или выберите ячейку D12 и откройте селектор визуальных данных с помощью Формулы > Дополнительные функции > STDEV .

Оценка стандартного отклонения на основе примера. Стандартное отклонение — это показатель того, насколько широко значения расходятся от среднего значения (среднего).

Эта функция была заменена на одну или несколько новых функций, которые могут обеспечить улучшенную точность и имена которых лучше отражают их использование. Эта функция по-прежнему доступна для совместимости с более ранними версиями Excel. Однако, если обратная совместимость не требуется, необходимо использовать новые функции с этого времени, так как они более точно описывают свои функции.

Дополнительные сведения о новой функции см. в StDev_S методе.

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных. Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

Remarks

STDEV assumes that its arguments are a sample of the population. If your data represents the entire population, then compute the standard deviation using STDEVP.

The standard deviation is calculated using the «n-1» method.

Arguments can either be numbers or names, arrays, or references that contain numbers.

Logical values and text representations of numbers that you type directly into the list of arguments are counted.

If an argument is an array or reference, only numbers in that array or reference are counted. Empty cells, logical values, text, or error values in the array or reference are ignored.

Arguments that are error values or text that cannot be translated into numbers cause errors.

If you want to include logical values and text representations of numbers in a reference as part of the calculation, use the STDEVA function.

STDEV uses the following formula:

where x is the sample mean AVERAGE(number1,number2,…) and n is the sample size.

Stdev Function Example

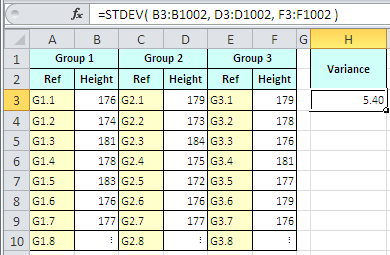
Imagine you want to find the standard deviation of the heights of adult males in London. It is not realistic to measure the height of all males, but you could take a sample of the population and measure their heights.

The example spreadsheet on the rightabove stores the measurements (in cm) of 3,000 adult males. The measured heights are stored in cells B3-B1002, D3-D1002 and F3-F1002.

=STDEV( B3:B1002, D3:D1002, F3:F1002 )

As shown in cell H3, the standard deviation in the individual heights of the sample group is calculated to be 5.40 cm.

Other Argument Types

In the example above, the arguments to the Stdev function are input as 3 cell ranges. However, you can also input figures directly, as individual numbers or number arrays.

For example, if you wanted to include two further heights, of 176cm and 177cm into the sample, you could add these directly into the above function as follows:

=STDEV( B3:B1002, D3:D1002, F3:F1002, 176, 177 )

=STDEV( B3:B1002, D3:D1002, F3:F1002, {176,177} )

For further information and examples of the Excel Stdev function, see the Microsoft Office website.

Как рассчитать дисперсию в Excel?

Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.

Рассчитаем дисперсию:

Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.

Точных вам прогнозов!

• Novo Forecast Lite — автоматический расчет прогноза в Excel .
• 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
• Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Практическое использование функции STDEV

Функции STDEV и STDEV.S обеспечивают оценку набора стандартных отклонений данных. Функция предполагает, что введенные числа представляют только небольшую выборку из всей изучаемой популяции. В результате он не возвращает точное стандартное отклонение. Например, для чисел 1 и 2 функция STDEV в Excel возвращает приблизительное значение 0,71, а не точное стандартное отклонение 0,5.

STDEV и STDEV.S полезны, когда тестируется только небольшая часть всего населения. Например, если вы тестируете изготовленную продукцию на соответствие среднему значению (для таких мер, как размер или долговечность), вы не можете протестировать каждую единицу, но вы получите оценку того, насколько варьируется каждая единица во всей совокупности от среднего.

Чтобы показать, насколько близки результаты для STDEV к фактическому стандартному отклонению (с использованием приведенного выше примера), размер выборки, использованный для функции, был менее одной трети от общего объема данных. Разница между расчетным и фактическим стандартным отклонением составляет 0,02.

• Error from midi driver fl studio что делать

    

• 1с деньги настройка синхронизации

    

• Как в ворд оф тенкс серебро поменять на золото

    

• Как удалить icloud apple id с iphone если забыл пароль

    

• Программа unknown для андроид